Camera Equivalence
– White Paper –
LumoLabs (fl)
|
Version: |
Feb 22, 2012, v1.1 |
|
Status: |
Final |
|
Print version: |
www.falklumo.com/lumolabs/articles/equivalence/CameraEquivalence.pdf |
|
Publication URL: |
|
|
Public comments: |
This White Paper tries to set common grounds when discussing various aspects of the effect of a change of the size of an imaging sensor in a digital camera system.
1. The "problem"
A recurring question is that about the influence of the sensor size in a camera on the quality of photography it can produce. I try to clarify a bit.
There is an article on Luminous Landscape I recommend:
www.luminous-landscape.com/essays/Equivalent-Lenses.shtml. Unfortunately, it is rather long as a concept and rather time-consuming to read. Also, the term "lens equivalents" is a bit confusing because we have to talk about camera equivalents, actually. Cameras take images, not lenses.
So, here is the problem: Given two cameras 1 and 2 (which I refer to as "reference" and "crop" camera, resp.) with their respective parameters which are field of view (angle of view) FoV, focal length f, lens aperture diameter d, F-stop N, sensor diameter s, number of pixels #MP and sensitivity setting ISO, cf. Fig. 1). Then I want to know how to best translate the two cameras' parameters which shall differ in sensor size s. It has become common practice to call the ratio of sensor sizes s(reference) and s'(crop) the crop factor c,
crop-factor c = s / s'
The reason for that term is that, all other variables kept identical, a smaller sensor would crop out the inner part of the image captured by the reference sensor. Typically, the other sensor is smaller than the reference and c > 1. Sometimes then, the reference is referred to as "crop c=1".
In drawings and numeric examples, I use the other crop factor to be c=2. This happens to be roughly the ratio of sizes of a 35mm "full frame reference" sensor and a Four Thirds sensor. But it doesn't matter. The number 2 is just easy to deal with.
2. The "solution"
Obviously, a wrong comparison would be to compare the reference camera with a crop camera where onlythe sensor is smaller (cropped). Because then the images would be completely different as the FoVwould change. Moreover, we cannot change our shooting position because this would alter the perspective.
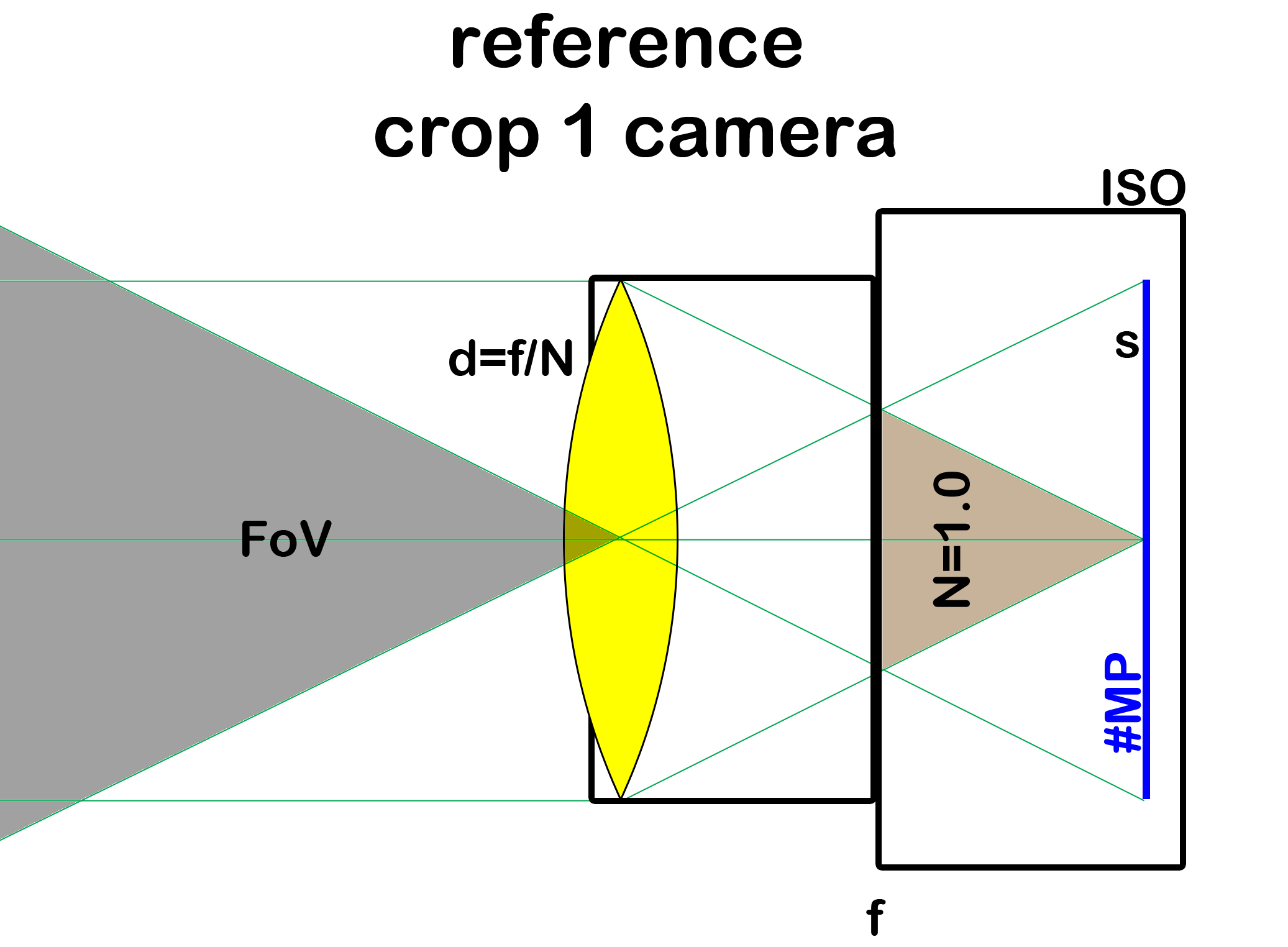
Fig. 1 Reference camera sketched with annotations for the image's field of view (angle of view) FoV, the lens' focal length f, lens' aperture diameter d, lens' F-stop N, the camera's sensor diameter sits number of pixels #MPand the camera's sensitivity setting ISO.
The lens is depicted yellow, the sensor blue. The F-stop Nis the ratio of focal length f and lens aperture diameter d: N = f / d
and can be visualized as the apparent size of the lens as seen from the sensor (brown shadowed area) where a narrower view means a higher F-stop or smaller relative aperture. The field of view FoV is depicted as the gray shadowed area, where a narrower view requires a tele lens.
In the image, N happens to be 1.0 and the FoV53°. But it doesn't matter.
The drawing splits the camera into two parts: the lens housing (left black rectangle) and the body (right black rectangle). Details like mirror or viewfinder are suppressed for clarity. The distance from the left edge of the body housing to the sensor is called flange or registration distance. We call it rbut it isn't very important for our argument. Moreover, the crop factor is c =1 because this is the reference camera where we consider any image it captures to be uncropped.
One way to achieve our goal seems to scale everything by 1:cwhich maintains the ratio of sensor size and focal length, i.e., the FoVdoesn't change (cf. Fig. 2).
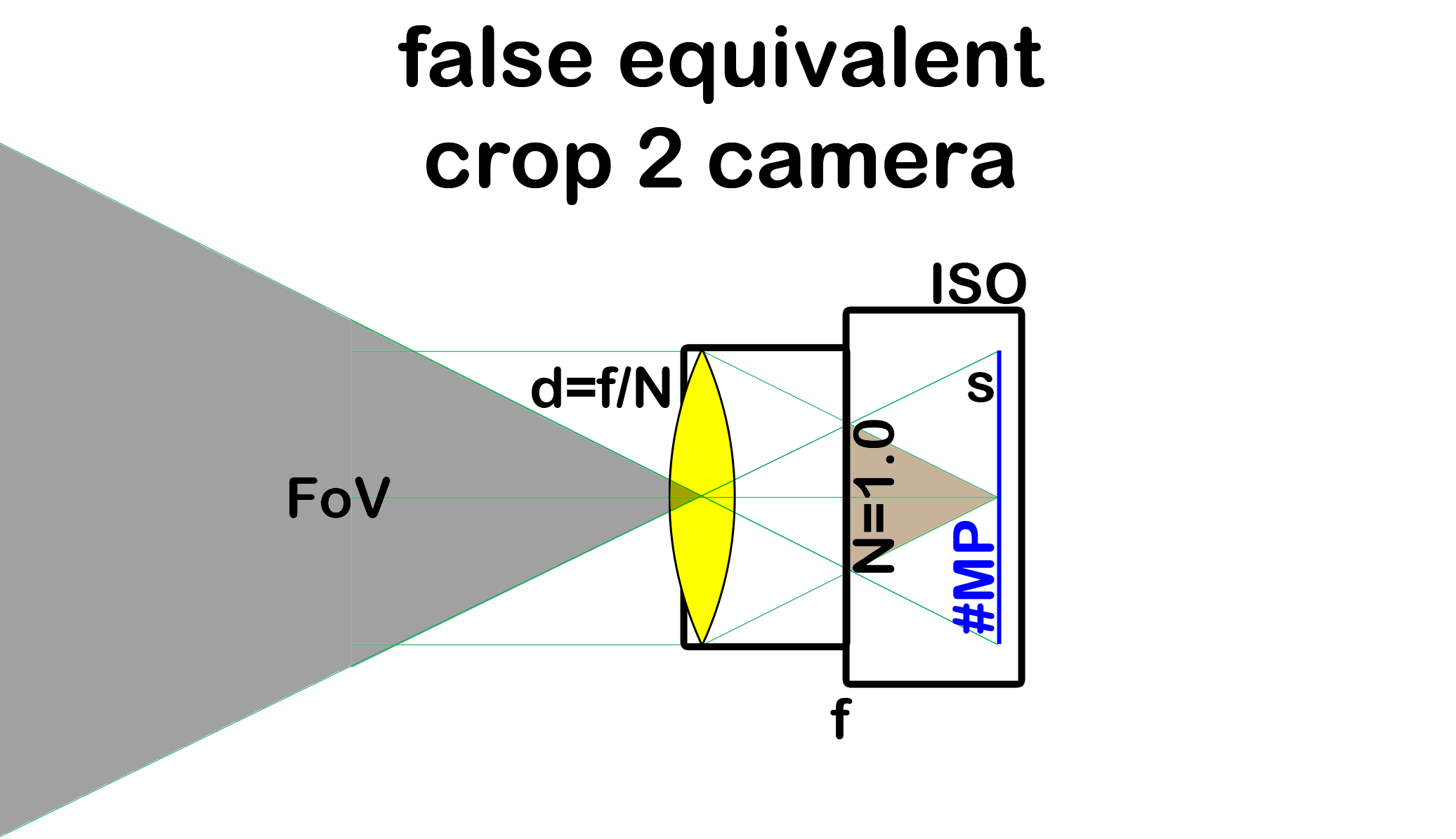
Fig. 2 Camera with crop c=2 which maintains the reference FoV: Everything is scaled to 50% size, FoV, F-stop N and ISOdon't change, the focal length is reduced to f' = f/c.
Often, this comparison is the starting point when comparing cameras with different sensor sizes. But it is wrong. Why?
Well, it can be shown (cf. later) that an image contains no information whatsoever to deduce the sensor size of the camera which took it! I.e., two cameras with different sensor sizes can (often) produce indistinguishable, or equivalent images which can't be told apart. But the two cameras shown above are notequivalent. E.g., the crop-2 camera would produce an image with more depth of field, more noise and more diffraction blur. Maybe, the field of view now is the same, but there are still image properties which changed. They are just a bit more subtle but they are there! This is why I call Fig. 2a "false equivalent camera". Because it isn't equivalent, only similiar.
The reason why Fig. 2(proportional scaling of all dimensions) does not yield an equivalent camera is that scaling in general does not preserve system properties! E.g., If you scale a human up to 10x its size, all its bones would break under its own weight. Because weight increases 1000x (by volume), bone strength however only increases 100x (by surface). So, when comparing camera systems with sensors of different size, a simple scaling doesn't do the job. Or as physicists would say, camera equivalence isn't scaling invariant :)
But what then is an equivalent camera with the sensor size changed?
As it turns out, the proper equivalent crop camera is obtained by scaling the focal length fand sensor size s as before, but notthe (absolute) lens aperture d(cf. Fig. 3)!
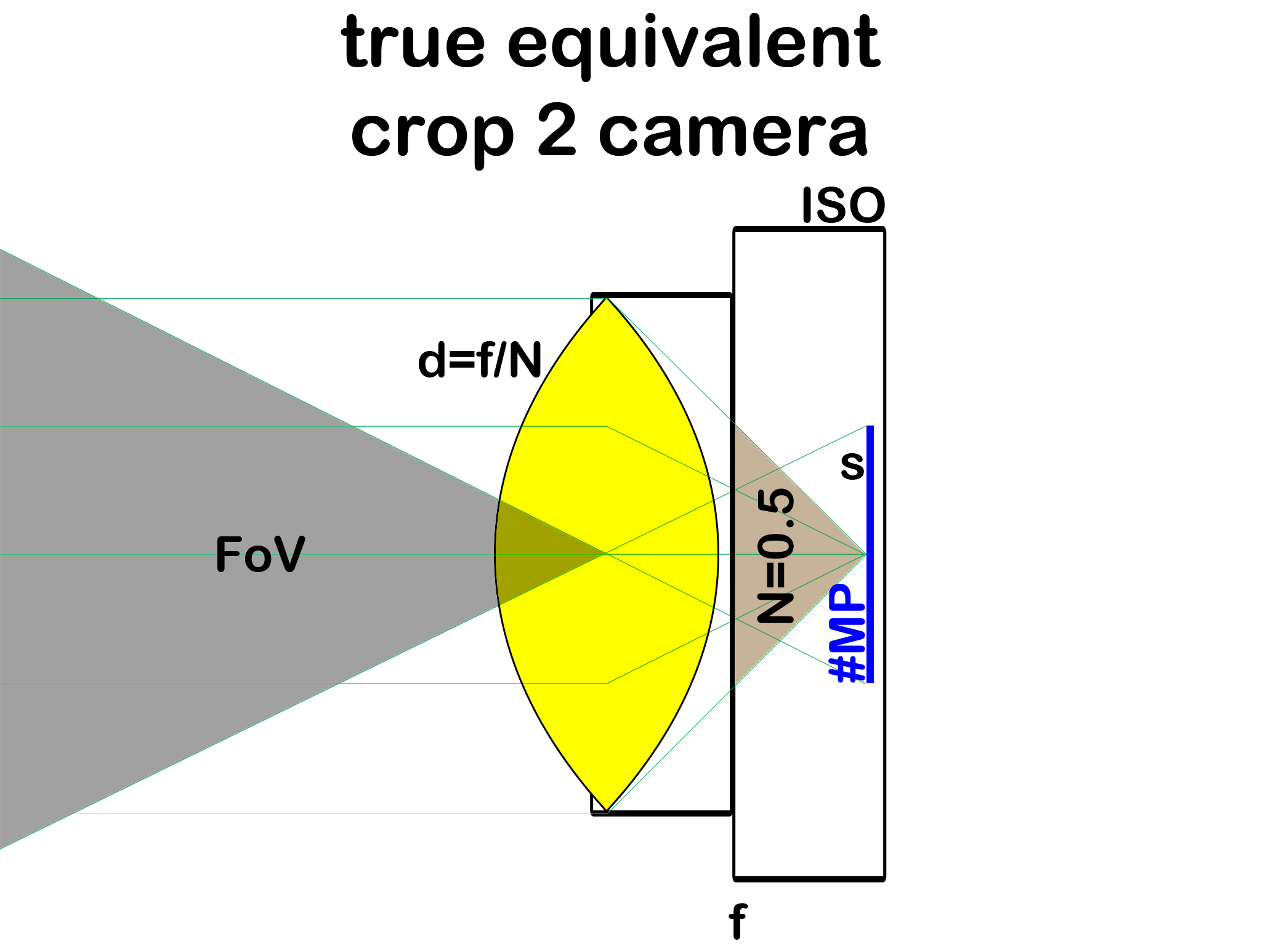
Fig. 3 Equivalent camera with crop c=2which maintains allimage properties: Only fand s are scaled to 50% size.
Because the glass' refraction index cannot be scaled, the yellow lens is drawn thicker to illustrate that the lens' refractive power doubled; or more precisely, that lens surface curvature radii need still be scaled to 50%.
Because f scales but d is kept a constant, N = f/d needs to scale with f.
The exact equivalence relationship between the reference camera and crop camera' is as follows:
-
-
s
= c s'
FoV
= FoV'
f
= c f'
d
= d'
N
= c N'
ISO
= c2 ISO'
#MP (type 1)
= #MP'
#MP (type 2)
= c2 #MP'
-
The relationship is written to derive the reference system properties for a given crop factor c, e.g., a reference system would have focal length f=50mmif the crop-2 system had f'=25mm.
There are two variations of the #MP relation (1) and (2). I will refer to the two variants as type-1 and type-2 equivalence, resp. I'll need it later only. If I say nothing, type-1 is meant or the type doesn't matter.
3. Properties of equivalent camera systems
A reference camera and a (true) equivalent camera produce respective images (assuming using ideal lenses on both cameras) which share the following properties (assuming type-1 equivalence):
-
Perspective
-
Field of View
-
Defocus blur, incl.:
-
Depth of Field (subject depth appearing focussed in a printed photo)
-
Background blur (blur of (infinity) subjects when out of focus)
-
-
Diffraction effects (blur due to diffraction)
-
Detail, resolution, number of pixels
-
Image noise (pixel noise due to photon shot noise)
-
Dynamic range
For this reason, it is impossible to tell the images apart. Which in turn means that sensor size is notan image property. Which in turn means that two camera systems with different sensor sizes must firstbe set-to / used-with equivalent parameters before they can be compared. Because otherwise, we are onlyseeing the inequivalence of choosen parameters and cannot learn anything from a comparison, except that, well cameras haven't been equivalent what was known á priori.
A camera setting is fullydescribed by either of the following parameter sets (including exposure time t):
-
t, d, FoV, #MP (4 independent parameters)
-
s, f, N, ISO, #MP (4 independent reference camera's parameters, with a given sensor size s)
-
s', f', N', ISO', #MP' (a crop camera's 5 parameters with a variable sensor size s').
So, either the real focal length f', aperture N', sensitivity ISO' and sensor size s' are specified, or the equivalent focal length f, aperture N, sensitivity ISO for a reference-sized sensor, e.g., 35mm film. It is a false specification to mix, like to specify f and N' (typical for P&S spec sheets), or f & N mixed with ISO' (typical for APS-C vs. full frame discussions).
Because the equivalent parameter set has one less parameter, it is the preferred way to specify a camera setup, consisting of "35mm-equivalent" (f, N, ISO):
-
"35mm-equivalent focal length" f
-
"35mm-equivalent F-stop" N
-
"35mm-equivalent" sensitivity ISO
Only the first value however, is currently written into EXIF image headers. I didn't include the #MP into this because most pixels remain invisible typically when printing to a normalized print size.
3.1. Proof of equivalence
Now, I would have to proof my claim above. I don't do, it would just obfuscate my point. I did the math and the above is the result. But there is a way to understand at least a few of the bullet points above in an intuitive manner working around the necessity to doing any math. Here we go.
I think we all can understand easily why perpective and field of view don't change. Now, consider the following question: How many photons are captured and make up the image, in total? Well, it is all photons flying (while the shutter is open) towards the camera from within the field of view, and hitting the lens' aperture. All of them eventually reach the sensor as it is how we define field of view here. And because we keep the lens' aperture diameter da constant, this number of photons is indeed a constant too. Which immediately yields that dynamic range and image noise is a constant too. Sensor size is no factor anymore! Moreover, the ISOsetting has to change because the illumination per sensor surface changes (photon density on the sensor changes) and we have to compensate to keep the exposure time ta constant. As we see, image noise from cameras with different size sensors should not be compared at the same ISO setting. Btw., that's a basic fact that is often overlooked (the only useful exception is pixel noise for type-2 equivalence; but it has no photographic meaning, only a technological one to compare the CMOS silicon processes).
To derive equivalence for depth of field and diffraction is a bit less straightforward. Diffraction equivalence can be derived w/o math when one knows that it is a direct result of the Heisenberg uncertainty relation and angular blur (momentum uncertainty) results from the finite absolute aperture (space constraint). No sensor size here again ;) And depth of field follows similar arguments, or one does the math. The shortest mathematical treatment follows the principle to make properties dimensionless first, like CoC/s which typically is chosen to be 1/1730.
3.2. Examples of equivalent cameras
I use type-2 equivalence for number of pixels for more entertainment.
|
|
Apple iPhone 4 |
Olympus E-5 |
Nikon D800 |
|||||||||
|
c |
f |
N |
ISO |
#MP |
f |
N |
ISO |
#MP |
f |
N |
ISO |
#MP |
|
7.64 |
3.85 |
2.8 |
80 |
5.0 |
4-9 |
0.5 |
7 |
0.8 |
3-9 |
0.4 |
2 |
0.6 |
|
2.00 |
15 |
11 |
1200 |
73 |
14-35 |
2.0 |
100 |
12.3 |
12-35 |
1.4 |
25 |
9 |
|
1.00 |
29 |
21 |
4700 |
290 |
28-70 |
4.0 |
400 |
49 |
24-70 |
2.8 |
100 |
36 |
As you can see, the 14-35/2 µFT and 24-70/2.8 Nikon FX lenses are not equivalent as the µFT lens would need an f/1.4 aperture and 2mm more zoom at the wide end to be. Both lenses are famous for their optical quality (for the given #MP). Nevertheless, the larger Nikon lens is less expensive and below, I am going to explain why.
Moreover, the reach advantage of the E-5 over the D800 is sqrt(49/36)or 1.17x as opposed to 2.0 which is the crop factor. Despite the name "crop" factor, it doesn't express a camera's cropping power. E.g., a cropped 300 mm lens on the E-5 is type-2 equivalent to a 350 mm lens on the D800.
4. Size matters
Now, I may have created the impression that sensor size does not matter. Because whatever be the size, cameras can be made equivalent. Wait a second, contrary to what you are being told, size matters indeed!
The reason is that not every parameter is feasible, there are constraints. E.g., consider the popular 35mm-equivalent (50mm, f/1.4, ISO 100) camera:
At c=2, the equivalent crop-2 camera would be a FourThirds (25mm, f/0.7, ISO 25) camera. Even though the Voigtlander Nokton 25mm f/0.95 MircoFourThirds (µFT) lens exists, it is very expensive (about 4x) and no µFT camera sports less than ISO 160 while we would need ISO 25 for equivalence. So, while the equivalent crop-2 camera exists on paper, it doesn't in practice. And its close approximations are expensive which is typical when approaching the constraints of a parameter space.
The constraints are as follows:
-
N' > 0.95 (N' > 1.2 for SLR designs)
this ignores the loss of optical performance when lowering N, typically below f/4 or f/2.8. -
ISO' > 50
The lower ISO value is defined by a sensor pixels's "full well capacity" divided by the pixel's light sensitive surface. One could visualize it as the "depth" of a pixel's well to collect electrons in. It is increasingly expensive to make an imaging sensor "thicker", leading to a constraint. However, I feel that ISO 25 and less for smallish sensors would be feasible if there would be more awareness about camera equivalence and a corresponding demand. -
Pixel pitch (s'/√#MP') > 1.2 µm
Constraint 1 leads to a diffraction constraint of 0.3 µm; but silicon process technology and the difficulty to build a diffraction-limited N=1 lens shifts the constraint well above 1 µm. With an SLR-like registration distance (45 mm), a reasonable limit raises to about twice this. -
d' < 67 mm (d' < 43 mm for CMOS)
Current limits due to current silicon process parameters. -
Sparsity of actually existing options on the market
E.g., a sensor-size comparison must take a vendor's actual set of choices into account.
In general, the sensor size does not affect image quality with equivalent parameters, all sensor sizes within one so-called equivalence class deliver indistinguishable images.
But within a given equivalence class of cameras (a given image quality, so to speak), making the sensor smaller reduces sensor cost and increases lens cost. In order to see why a smaller sensor increases lens cost, consider that the diameter d is kept constant (so, the main cost factor doesn't change) but lens elements become thicker (or more numerous) and have to be made on tighter tolerances. Lens and sensor cost functions aren't linear, which means that when cost from both factors is added, the resulting curve first decreases (as a function of sensor size), hits a minimum (the sweet spot) and then increases again for sensor sizes beyond the sweet spot. You get a curve with infinite cost for impossible parameters and a sweet spot for sensor size where cost is minimal.
Therefore within this equivalence class, sensor size may be too small or too large with respect to the sweet spot for a camera when looking for an optimum price performance ratio. There is a sensor size which optimzes overall cost for a given equivalence class of cameras. Of course, this size is a function of time because sensor cost and lens cost vary on different time scales. Over time, the sweet spot crawls towards larger sensor sizes.
And there are always equivalence classes of cameras where the sweet spot is at a P&S size and where the sweet spot is at medium format size. So, one would have to agree on relevantequivalence classes of cameras to make a verdict about any given sensor size. Obviously, this agreement will vary largely from photographer to photographer.
Note again that an equivalence class of cameras is defined by "35mm-equivalent focal length", "35mm-equivalent F-stop" and "35mm-equivalent" sensitivity. E.g., "P&S" does notdenote an equivalence class of cameras. In practice, the first parameter is irrelevant for an interchangeable lens camera and the other two are limits, e.g., read minimum 35mm-equivalent F-stop (maximum available lens diameters in mm for a given FoV) and minimum 35mm-equivalent sensitivity (maximum dynamic range). Note that there is no maximum sensitivity limit, sensitivity can be dialed to infinity, it is the noise which matters and noise is already defined by the lens diameter in mm.
4.1. Large is a superset of small
All of this means that a larger sensor is an element in more equivalence classes of cameras than a smaller sensor. But is it a true superset?
Well, for type-2 equivalence, it actually is!
Type-2 equivalence scales #MP by c2. So with type-2 equivalence, a crop-2 12 MP camera would be in a 35mm-equivalent 48 MP class. Something, the Nikon D800 comes actually close to.
One may fear that this reduction of the pixel pitch may negatively affect image noise and would break the equivalence because now less photons will reach a pixel. However, it can be shown exactly (for photon shot noise) and empirically (for combined readout noise etc., cf. DxO laboratories for a reference) that all effects cancel out at the image level, i.e., this is not the case.
Without going into too much detail, just consider that 4 pixels combined have 4x the signal but only 2x the noise (sqrt(12+12+12+12)). Similiar arguments apply for readout noise and micro lenses compensate for a loss of fill factor (wiring reducing a pixel's relative image sensitive area).
Type-2 equivalence has the same properties as claimed for type-1 equivalence above, except that resolution now increases with sensor size. With type-2 equivalence, we obtain the following:
-
The same "reach" or cropping power than with a smaller sensor:
The same focal length doesn't act as a longer effective focal length with a smaller sensor, because the cropping power only depends on the pixel pitch, not the crop factor. -
The same maximum depth of field
When stopping down with a larger sensor, higher F-stop N are required for equivalence. One may fear they don't exist on the end of maximum depth. However, the minimum aperture size which the blades can be shut down to is typically rather invariant, meaning that longer focal lengths can be shut down more when expressed in terms of F-stops. This exactly cancels out the effect.
(actually, we don't need type-2 equivalence here)
So, with "reach" and "deep field" having the same upper limits for type-2 equivalence, we found that a larger sensor provides a full superset of available equivalent parameters over those of a smaller sensor.
Moreover, a "type-2" sensor with more megapixels won't cost significantly more. It is sensor area and its total full well capacity which are dominating overall cost. The only effect may be on the speed of image processing. But then, image processors typically don't drive overall cost.
4.2. Non-ideal lenses
So far, we considered camera equivalence with ideal lenses. In practice they don't exist.
So, let's briefly look at the performance of equivalent cameras with non-ideal lenses. This can't be treated in an exact manner. But we can still approximate the issue.
4.2.1. Center performance
At the center, I empirically derived from photozone.de data that best lenses resolve about 100 N g(f) lp/mm (line pairs per millimeter) in the center before taking diffraction and finite sensor resolution into account. We treated sensor resolution and diffraction before, it is constant within a class of (type-1) equivalence.
I found g(f) to be a function varying slowly with the focal length f, like g(f) ~ sqrt(50mm/f). Theoretically, for lenses of equal construction, g(f)should be linear in 1/f(corresponding to a constant angular resolution). But larger fseem to allow for countermeasures like tighter relative manufacturing tolerances or another corrective lens group, esp. if the widest F-stop is higher. This particularly holds true for lenses which cannot fully scale because of a given registration distance.
Observing that lp/mm is an absolute figure, N increases with the sensor size and image magnification decreases with sensor size, we have a relative LW/PH (line width per picture height) center resolution which scales like ~s3/2. Or effective megapixels (in the center) scale like
MP (effective, center) = ~sp< diffraction limit with ~2.5 < p< ~3.5
meaning that the diffraction limit is reached more easily. Center performance benefits more than linearly with the sensor size, up to the point where a lens becomes diffraction limited. Pixel resolution in the center with a larger sensor is even slightly improved with type-2 equivalence where the larger sensor has more pixels as long as one stays well below the diffraction limit. But of course with type-2 equivalence, pixel noise is stronger at the same time.
Overall, equivalent center lens performance strongly decreases with the crop factor as soon as the lens isn't diffraction limited anymore. Stopped down enough, the difference disappears.
4.2.2. Corner performance
Corner performance is more difficult to judge. Aberrations increase with the distance from the center, sometimes with the square of this distance. On the other hand, this decrease starts at a higher center performance and the angular distance of corners from the optical axis actually doesn't increase for equivalent cameras. So, there are two effects working in opposite directions.
Because of the complexity of existing optical constructions, I decided to empirically check two type-2 equivalent cameras with published results and lenses of similar quality.
I use the photozone.de tests on the D200 (DX) and D3X (FX= which have about the same pixel pitch (are type-2 equivalent). Unfortunately, photozone.de uses different sharpening parameters (or the D3X has a weaker AA filter which is the same) so results are not directly comparable. Using the Nikkor AF-S 200/2G at f/2.8 as reference calibration point (2242 LW/PH DX vs. 4076 LW/PH FX), I however just need to add a square extra blur kernel of 4087 LW/PH DX after scaling the FX results to DX using c=1.52 (cf. my LumoLabs paper "Understanding Image Sharpness" to understand how a direct comparison is feasible):
1/22422= (1.52/4076)2+ 1/40872
Corner performance is of most concern at wider apertures and FoV. So, I select a corresponding APS-C (DX) lens with interesting corner performance: Nikkor AF-S 24/1.4G. It actually is an FX lens but better than all dedicated DX lenses in this range. I used this lens too because an almost equivalent lens exists for FX: Nikkor AF-S 35/1.4G (equivalent would be 36 mm).
|
Corner Performance DX |
Nikkor AF-S 24/1.4G |
Nikkor AF-S 35/1.4G |
Corner Performance FX |
|
1.4 |
1087 |
1732 (*) |
2.0 |
|
2.0 |
1306 |
1807 (*) |
2.8 |
|
2.8 |
1601 |
1917 (*) |
4.0 |
|
Vignetting DX |
|
|
Vignetting FX |
|
1.4 |
0.71 |
1.35 |
2.0 |
|
2.0 |
0.32 |
0.64 |
2.8 |
|
2.8 |
0.19 |
0.43 |
4.0 |
|
Border CA DX |
|
|
Border CA FX |
|
1.4 |
1.27 |
1.95 |
2.0 |
|
2.0 |
1.24 |
1.89 |
2.8 |
|
2.8 |
1.18 |
1.75 |
4.0 |
The peak performance of both lenses in the center (when calibrated to DX resolution) is similar: 2192 (*) (AF-S 35/1.4 on FX) vs. 2180 (AF-S 24/1.4 on DX) showing that calibration worked ok.
The numbers in the table above are LW/PH for the DX format (APS-C). The (*) designates that numbers are renormalized to photozone.de's D200 test camera using the calibration explained above. Vignetting is given in EV, Border CA in pixels which have similar size.
So, this little exercise shows that camera's with increasing crop factor suffer in corner resolution too. Within a given class of equivalence, corner and edge resolution increases with increasing sensor size. Not as fast as the center performance does. But if center performance is already diffraction-limited, the difference may actually still be visible in the corners with an advantage for the larger sensor. Other effects like vignetting or chromatic aberrations seem to decrease with increasing crop. I assume both are basically independent of the sensor size when doing a proper analysis.
I assume that lenses optimized for a given image circle and with a scaled registration distance (as is possible with mirrorless systems) allow for a corner performance of equivalent cameras which is just independent of the sensor size. I am aware that only few direct comparisons of corner performance of equivalent cameras have been published so far. But the little exercise above while preliminary is already quite conclusive:
It is a myth that APS-C cameras "crop the sweet spot" of the image field of lenses which cover a larger image circle or are made for a full registration distance.
4.3. Non-ideal camera bodies
I cannot discuss all possible deviations from an ideal camera, as are produced by shutter blur, mount calibration, focus screen calibration, AF calibration, non-parallel sensor assemblies etc. But one effect triggered my particular interest:
4.3.1. Phase detect autofocus performance
Phase detect autofocus (PDAF) works by aligning two patterns created from subimages through the lens which are separated by an angular distance NAF, where NAF expresses this angular distance as an F-stop which would have the same angular width.
Most PDAF detectors have NAF=5.6. Some cameras (esp. more expensive ones) replace a single central NAF=5.6 detector by two detectors, one being NAF=2.8 and another being NAF=8.
We will assume a constant average error in pattern alignment achieved by the PDAF module for a given NAF within a class of equivalent cameras (e.g., identically made PDAF detectors). This results in a constant average error e in focus plane positioning where accuracy (1/e) is proportional to the AF detectors' aperture, e = E NAF. This is independent of the lens' focal length as long as the mechanical focus mechanism's accuracy isn't the limiting factor. We also ignore sperical aberration or assume that the firmware contains a correction lookup table.
A typical value for E is 5–10 µm. But it also depends on luminosity, contrast and the quality of the PDAF module (assuming a perfect calibration).
This defocus e causes a defocus blur (expressed as diameter of a circle of confusion CoC):
CoC = e / N
where N is the image's F-stop. The corresponding image blur, scaled to the image size, then is:
CoC' / s' = E NAF / (s'N') = c2 E NAF / (sN) ~ c2 NAF
In order to compensate, NAF would have to scale with 1/c2. Unfortunately, rather the opposite is true, full frame cameras have NAF=2.8 detectors while APS-C cameras have NAF=5.6 detectors when it rather should be the other way around for equivalent performance. This means that in real life, an equivalent full frame camera will achieve 2x – 4x better focus accuracy than an APS-C camera using the same PDAF module technology.
For contrast AF autofocus (CDAF), the dependency is only linear in c, CoC'/s' ~ c. Assuming equivalent lenses are used. Otherwise, the larger lenses would be stopped down more.
We find that autofocus performance is strongly sensor size dependent for equivalent cameras. Personally, I consider focussing to be a main area where sensor size does actually matter.
4.3.2. Manual focus and optical viewfinder
It is often stated that a larger sensor camera allows for an optical viewfinder of better quality. Well, for equivalent cameras, this is not true. The viewfinder magnification just has to scale with c. For an equivalent camera, the viewfinder image then doesn't become darker nor smaller.
It is a lack of equivalent lenses and the attempt to save cost that such cameras don't exist.
This lack of options cause an artificial advantage for the larger sensor. Nevertheless as explained above, more care would be needed with a smaller sensor to calibrate an equivalent viewfinder's focus screen to allow for an equally precise manual focus operation. Care which in practice is rare.
5. Conclusion
Sensor size plays no rôle as long as different cameras use equivalent parameters which implies a scaling of focal length, F-stop and ISO sensitivity. This holds true for "ideal" cameras which fully exploit the laws of nature.
In any comparison of different cameras, parameters should first be made equivalent in order to conclude non-trivial statements. I.e., scaling focal length, but not F-stop and/or ISO sensitivity must lead to trivial statements.
With equivalent scaling, all comparisons then amount to deviations from the ideal nature of a camera. This includes cost for a given performance or performance for a given cost or available options on the market. It was explained that the sweet spot where cost optimizes performance crawls to increasing sensor sizes, as performance requirements increase or technological progress advances, both effects being independent but amplifying each other.
Eventually, it was shown that cameras with a larger sensor form a superset of cameras with a smaller sensor if the pixel pitch is kept constant. As long as two cameras are in the intersection of both sets, they produce images which are indistinguishable.